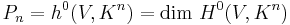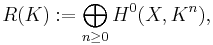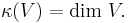Kodaira dimension
In algebraic geometry, the Kodaira dimension κ(V) measures the size of the canonical model of a projective variety V.
The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar (Igor R. Shafarevich, B. G. Averbuh & Ju. R. Vaĭnberg et al. 1965).
Contents |
The plurigenera
The dimension
is the classically-defined n-th plurigenus of V. The pluricanonical divisor 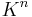 , via the corresponding linear system of divisors, gives a map to projective space
, via the corresponding linear system of divisors, gives a map to projective space
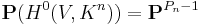 ,
,
called the n-canonical map.
Kodaira dimension
The canonical ring R=R(K) of a variety V is the graded ring
where K is a canonical divisor of V. The projective dimension of R(K) is called the Kodaira dimension.
Definition
The following are equivalent:
- The dimension of the Proj construction
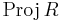 (this variety is called the canonical model of V).
(this variety is called the canonical model of V).
- The dimension of the image of the n-canonical mapping for n large enough.
- The transcendence degree of R, minus one, i.e. t − 1, where t is the number of algebraically independent generators one can find.
- The rate of growth of the plurigenera: it is the smallest number κ such that
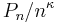 is bounded. In Big O notation, it is the minimal κ such that
is bounded. In Big O notation, it is the minimal κ such that 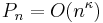 .
.
Conventionally, when R is trivial (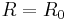 = underlying field (constant functions); the plurigenera are all zero (other than
= underlying field (constant functions); the plurigenera are all zero (other than 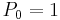 ); the pluricanonical divisors are not effective), which happens for example when V is rational, one takes
); the pluricanonical divisors are not effective), which happens for example when V is rational, one takes 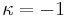 (in agreement with the transcendence degree definition), or sometimes
(in agreement with the transcendence degree definition), or sometimes 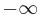 (which is a conventional dimension of the empty set, as it preserves additivity under multiplication).
(which is a conventional dimension of the empty set, as it preserves additivity under multiplication).
Kodaira dimensions can take any value from −1 to the dimension of V.
Application
The Kodaira dimension is a relatively coarse invariant, and helps to give the outline for the classification of algebraic varieties: it is coarse in that there are generally several distinct families of varieties with a given Kodaira dimension.
Varieties with low Kodaira dimension are special, while varieties of maximal Kodaira dimension are (suggestively) called general type.
Geometrically, there is a rough correspondence between Kodaira dimension and curvature: negative Kodaira dimension corresponds to positive curvature, zero Kodaira dimension corresponds to flatness, and maximum Kodaira dimension (general type) corresponds to negative curvature.
The specialness of varieties of low Kodaira dimension corresponds to the specialness of Riemannian manifolds of positive curvature (and general type corresponds to the genericity of non-positive curvature); see classical theorems, especially on Pinched sectional curvature and Positive curvature.
The above statements are made more precise below.
Dimension 1
Complex non-singular algebraic curves are discretely classified by genus, which can be any natural number 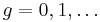 .
.
By "discretely classified" we mean that for a given genus, there is a connected, irreducible moduli space of curves of that genus.
The Kodaira dimension of an algebraic curve is:
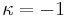 : genus 0 (projective line): K is not effective,
: genus 0 (projective line): K is not effective, 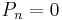
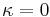 : genus 1 (elliptic curves): K is a trivial bundle,
: genus 1 (elliptic curves): K is a trivial bundle, 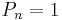
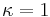 : genus 2 or more: K is ample.
: genus 2 or more: K is ample.
Compare with the Uniformization theorem for surfaces (real surfaces, which are the analogue in differential geometry of algebraic curves): Kodaira dimension -1 corresponds to positive curvature, Kodaira dimension 0 corresponds to flat, Kodaira dimension 1 corresponds to negative curvature. Note that the generic surface is of general type: in the moduli space of surfaces, 2 components have Kodaira dimension below 1, while all other components have Kodaira dimension 1. Further, the component corresponding to genus 0 is a point, to genus 1 is 1-dimensional, and to genus 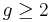 is
is 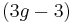 -dimensional.
-dimensional.
Dimension 2
The Enriques-Kodaira classification classifies surfaces: coarsely by Kodaira dimension, then in more detail within a given dimension.
General dimension
Rational varieties have negative Kodaira dimension (corresponding to positive curvature). Abelian varieties and Calabi-Yau manifolds (in dimension 1, elliptic curves; in dimension 2, complex tori and K3 surfaces) have Kodaira dimension zero (corresponding to admitting flat metrics and Ricci flat metrics, respectively).
General type
A variety of general type V is one of maximal Kodaira dimension (Kodaira dimension equal to its dimension):
Equivalently, K is a big line bundle; equivalently, the n-canonical map is generically injective for n sufficiently large.
For example, a variety with ample canonical bundle is of general type.
In some sense varieties of general type are generic, hence the term (discrete invariants of varieties of general type vary in more dimensions, and moduli space of varieties of general type have more dimensions; this is made more precise for curves and surfaces). A smooth hypersurface of degree d in the n-dimensional projective space is of general type if and only if d is greater than n+1. In this sense most smooth hypersurfaces in the complex projective space are of general type.
Varieties of general type seem too complicated to classify explicitly, even for surfaces.
Siu (1998) proved invariance of plurigenera under deformations for varieties of general type.
Application to classification
The Iitaka conjecture states that the Kodaira dimension of a fibration is at least the sum of the Kodaira dimension of the base and the Kodaira dimension of a general fiber. This motivates a classification programme for algebraic varieties, in which it is sought to represent V as a fibration over a variety of general type, with typical fiber of Kodaira dimension 0. This is quite a natural idea, given that the application of the Proj construction to the pluricanonical ring should produce a projective variety in which the sections of powers of K 'capture' as much as they can about V.
See also=
References
- Dolgachev, I, (2001), "Kodaira dimension", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=K/k055630
- Shafarevich, Igor R.; Averbuh, B. G.; Vaĭnberg, Ju. R.; Zhizhchenko, A. B.; Manin, Ju. I.; Moĭshezon, B. G.; Tjurina, G. N.; Tjurin, A. N. (1965), "Algebraic surfaces", Akademiya Nauk SSSR. Trudy Matematicheskogo Instituta imeni V. A. Steklova 75: 1–215, ISSN 0371-9685, MR0190143